INSTITUTO LA RIVERA : MATEMÁTICAS

17/09/2020 SEMANA 22

TERCER PERIODO

Dale click al siguiente link:

https://drive.google.com/file/d/17DbVmZ90C3t8jFE2MO98qOuyjhu-socA/view?usp=sharing

----------------------------------------------------------------

10/09/2020 SEMANA 21

Dale click al siguiente link:

https://drive.google.com/file/d/16AEtFhiQXrjWPgr_Ju6XniZ3vEYq5O5B/view?usp=sharing

-------------------------------------------------------------------------------

27/08/2020 – SEMANA 20

Dale click al siguiente link:

https://drive.google.com/file/d/18wm9RDSqZHPLMZ23wTunZmif1FZ-H25Y/view?usp=sharing

----------------------------------------------------------------------------------------

20/08/2020 SEMANA 19

MÁXIMO COMÚN DIVISOR

Dale click al siguiente link:

https://drive.google.com/file/d/14SyLj20vmB4cTxn0JY--HNflaJ9xr-Sg/view?usp=sharing

------------------------------------------------------------------------

13/08/2020 – SEMANA 18

DESCOMPOSICIÓN DE UN NÚMERO EN FACTORES PRIMOS

Dale click al siguiente link:

https://drive.google.com/file/d/10TJ_aJJbxnRMZqkFANBDEsZGPebfpzzr/view?usp=sharing

------------------------------------------------------------------------------------------------------------

06/08/2020 – SEMANA 17

CRITERIOS DE DIVISIBILIDAD

Dale click al siguiente link:

https://drive.google.com/file/d/1VycHRjdWAcw-r-DcAKh-a7y1JQDJfQbf/view?usp=sharing

---------------------------------------------------------------------------------------------------------------------------------

30/07/2020 – SEMANA 16

MÚLTIPLOS Y DIVISORES

Dale click al siguiente link:

https://drive.google.com/file/d/1TnUT-svG31oY7FOdyZNW_rZYFYCK4XHu/view?usp=sharing

---------------------------------------------------------------------------------

23 – 07 – 2020 – SEMANA 15

ECUACIONES

Dale click al siguiente link:

https://drive.google.com/file/d/15UZ-albDui7-BoaQXzLwxHx5g6fMusO4/view?usp=sharing

https://drive.google.com/file/d/15UZ-albDui7-BoaQXzLwxHx5g6fMusO4/view?usp=sharing

------------------------------------------------------------------------

16 – 07 – 2020 – SEMANA 14

LOGARITMACIÓN EN LOS NATURALES

Dale click al siguiente link:

https://drive.google.com/file/d/1gDaYavxTVnAvBW51oY50Dq5SiprWHV7d/view?usp=sharing

---------------------------------------------------------------------------------

09 – 07 – 2020 – SEMANA 13

OBJETIVOS:

· Utiliza las propiedades de los números enteros y racionales y las propiedades de sus operaciones para proponer estrategias y procedimientos de cálculo en la solución de problemas.

· Propone y utiliza diferentes procedimientos para realizar operaciones con números enteros y racionales.

RADICACIÓN EN LOS NATURALES

ACTIVIDAD

Dale click al siguiente link:

https://drive.google.com/file/d/1O-DPM1OvglHTizy1ooEzKP-V8TytifvN/view?usp=sharing

IMPORTANTE TENER EN CUENTA:

1. tomar foto de la transcripción de la información y la actividad desarrollada en el cuaderno, enviarla al correo murilloviviana82@gmail.com. Por favor enviar un solo correo con todas las fotos relacionadas a mis áreas.

2. fecha de entrega de la actividad desarrollada: LUNES 13 DE JULIO DEL 2020.

3. especificar: nombres, apellidos, grado del estudiante y materias.

----------------------------------------------------------------------------------

19 – 06 – 2020 – SEMANA 12

OBJETIVOS:

· Utiliza las propiedades de los números enteros y racionales y las propiedades de sus operaciones para proponer estrategias y procedimientos de cálculo en la solución de problemas.

· m Propone y utiliza diferentes procedimientos para realizar operaciones con números enteros y racionales.

RADICACIÓN EN LOS NATURALES

Radicacion de numeros naturales - TOMi.digital

Dale click al siguiente link:

https://drive.google.com/file/d/19FQS3J5_ayQut7flHzqr4FuP1cf23qZg/view?usp=sharing

https://drive.google.com/file/d/19FQS3J5_ayQut7flHzqr4FuP1cf23qZg/view?usp=sharing

-------------------------------------------------------------------------------------------------------------------------

12/06/2020 – SEMANA 11

Otras operaciones en el conjunto de los números naturales

POTENCIACIÒN EN LOS NATURALES

La potenciación es una operación... - Clases particulares de ...

ACTIVIDAD

1. Realiza los siguientes ejercicios en tu cuaderno

22 versículos bíblicos sobre la fe - Su Biblia

IMPORTANTE TENER EN CUENTA:

2. fecha de entrega de la actividad desarrollada: LUNES 15 DE JUNIO DEL 2020.

3. especificar: nombres, apellidos, grado del estudiante y materias.

--------------------------------------------------------------------------------------------------------------------------
08/06/2020 – SEMANA 11

Otras operaciones en el conjunto de los números naturales

POTENCIACIÒN EN LOS NATURALES

Propiedades de la potenciación – Mates Fáciles

La potenciación es una operación que permite escribir, en forma abreviada, productos cuyos factores son todos iguales. Así:

Ejemplo:

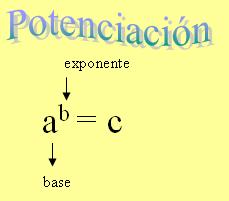
En la expresión, a recibe el nombre de base y es el factor que se repite; b recibe el nombre de exponente y es el numero de veces que se repite la base, y c recibe el nombre de potencia y es el resultado de multiplicar la base tantas veces como lo indica el exponente.

EL SÚPER HÉROE QUE HAY EN MI: TEMA 3. MULTIPLICACIÓN Y POTENCIAS

Cálculo de potencias y sus propiedades - Didactalia: material ...

Potencia de 10:

Las potencias de 10 son potencias que resultan de elevar el numero 10 a cualquier número natural. Por ejemplo, 1.000 es una potencia de 10 pues:

MATEMÁTICAS POTENCIAS DE NÚMEROS NATURALES ...

Propiedades de la potencia:

La potenciación es el conjunto de los números naturales, cumple con las siguientes propiedades:

El cero y el número en la potencia:

Cuando la base o el exponente de una potencia están relacionados con el número 0 y 1, se determinan las siguientes propiedades:

Expresiones con potencias:

Para solucionar una expresión que contenga potencias indicadas, se debe tener en cuenta que primero se resuelven dichas potencias para, luego, resolver las multiplicaciones y divisiones correspondientes en su orden respectivo. Por último, se resuelven las sumas y las restas presentes en la expresión.

Si la expresión presenta signos de agrupación, esto se debe eliminar de dentro hacia fuera, resolviendo las operaciones indicadas en cada uno de ellos.

10 Versículos sobre Promesas de Sanidad en la Biblia | Frases ...

------------------------------------------------------------------------------------------------------------
04/06/2020 – SEMANA 10

SEGUNDO PERIODO

Ejes temáticos:

1. Otras operaciones en el conjunto de los números naturales

2. Ecuaciones

3. números positivos y negativos

Teoría de números

1. Múltiplos y divisores

2. Números primos números compuestos

3. Máximo común divisor

4. Mínimo común múltiplo

Fracciones y decimales

1. Fracciones

Grafica del segundo periodo (1 hoja )

Ejemplos:

OBJETIVOS:

Utiliza las propiedades de los números enteros y racionales y las propiedades de sus operaciones para proponer estrategias y procedimientos de cálculo en la solución de problemas.

Propone y utiliza diferentes procedimientos para realizar operaciones con números enteros y racionales.

SOLUCIÓN DE EXPRESIONES ARITMÉTICAS

Para resolver una expresión sin signos de agrupación, primero se debe resolver:

1. Las multiplicaciones

2. Las divisiones

3. Las Sumas

4. Las restas

Para resolver una expresión con signos de agrupación, estos de se deben eliminar de adentro hacia afuera. Para esto se resuelven las operaciones indicadas dentro de cada uno de ellos.

ACTIVIDAD

Resuelve los ejercicios propuestos en la página 20, del libro rutas matemáticas.

36 Versículos de la Biblia sobre la Evangelización - DailyVerses.net

IMPORTANTE TENER EN CUENTA:

2. fecha de entrega de la actividad desarrollada: MARTES 09 DE MAYO DEL 2020.

3. especificar: nombres, apellidos, grado del estudiante y materias.

----------------------------------------------------------------------------------------------------------------------

8 – MAYO – 2020 – SEMANA 9

TALLER COMPROBATORIO

LINK DE ACCESO:

https://drive.google.com/file/d/1NXiFKGibQI1gAt3p0U9H8le26ckFEzHN/view?usp=sharing

IMPORTANTE TENER EN CUENTA:

2. fecha de entrega de la actividad desarrollada: VIERNES 22 DE MAYO DEL 2020.

3. especificar: nombres, apellidos, grado del estudiante y materias.

------------------------------------------------------------------------------------------------------------
11 – MAYO – 2020 – SEMANA 8

OBJETIVOS:

· Opera sobre números desconocidos y encuentra las operaciones apropiadas al contexto para resolver problemas.

· Utiliza las operaciones y sus inversas en problemas de cálculo numérico

· Realiza combinaciones de operaciones, encuentra propiedades y resuelve ecuaciones en donde están involucradas

DIVISIÓN DE NÚMEROS NATURALES

En la división de números naturales se presentan dos casos dependiendo del residuo. Estos dos casos son: división exacta y división inexacta.

ACTIVIDAD

Resuelve: pag 19 - rutas matemáticas

Mateo 6:33 - RVR60 - Versículo de la Biblia del día - DailyVerses.net

IMPORTANTE TENER EN CUENTA:

2. fecha de entrega de la actividad desarrollada: VIERNES 16 DE MAYO DEL 2020.

3. especificar: nombres, apellidos, grado del estudiante y materias.

--------------------------------------------------------------------------------------------------------------------------
04 – MAYO – 2020 – SEMANA 7

OBJETIVOS:

· Propone y utiliza diferentes procedimientos para realizar operaciones con números enteros y racionales.

· Argumenta de diversas maneras la necesidad de establecer relaciones y características en conjuntos de números (ser par, ser impar, ser primo, ser el doble de, el triple de, la mitad de, etc)

SOLUCIÓN DE EXPRESIONES ARITMÉTICAS

Una expresión aritmética es aquella en la que se combinan números naturales mediante diversas operaciones. Para resolver expresiones aritméticas se deben tener en cuenta los siguientes casos.

Operaciones combinadas de números naturales, prioridad o jerarquía ...

· Para resolver una expresión sin signos de agrupación, primero se debe resolver:

1.    Las multiplicaciones
2.    Las divisiones
3.    Las Sumas
4.    Las restas

Ejemplo: 9 * 5 + 18 ÷ 3 - 6 * 5

1. Se realizan las multiplicaciones, y se escribe las otras partes de la operación, que faltan por resolver, así:

= 45 + 18 ÷ 3 - 30

2. Se resuelven las divisiones así:

= 45 + 6 – 30

3. Se resuelven las sumas así:

= 51 – 30

4. Se resuelven las restas así:

= 21

· Para resolver una expresión con signos de agrupación, estos de se deben eliminar de adentro hacia afuera. Para esto se resuelven las operaciones indicadas dentro de cada uno de ellos.

Ejemplo: 15 + [9 ÷ (11 * 2 - 19)]

1. Se resuelven los productos del paréntesis, y se escribe las otras partes de la operación, que faltan por resolver así:

= 15 + [9 ÷ (22 – 19)]

2. Se eliminan los paréntesis efectuando la resta correspondiente así:

= 15 + [9 ÷ 3]

3. Se eliminan los corchetes efectuando la división indicada así:

= 15 ÷ 3

4. Se efectúa la suma correspondiente así:

= 18

Imágenes Cristianas – Jesús Mi Fiel Amigo | Mis Imagenes Cristianas

----------------------------------------------------------------------------------------------------------------------------------
27 - ABRIL - 20 --- SEMANA 6

OBJETIVOS:

Utiliza las propiedades de los números enteros y racionales y las propiedades de sus operaciones para proponer estrategias y procedimientos de cálculo en la solución de problemas.

Propone y utiliza diferentes procedimientos para realizar operaciones con números enteros y racionales

Argumenta de diversas maneras la necesidad de establecer relaciones y características en conjuntos de números (ser par, ser impar, ser primo, ser el doble de, el triple de, la mitad de, etc).

MULTIPLICACIÓN DE NÚMEROS NATURALES

Dados a, b, c, € N, se define la multiplicación o producto como a * b = c, donde a y b se denominan factores y c producto.

Por ejemplo, en la operación 7 * 4 = 28, 7 y 4 son los factores y 28 el producto .•

ACTIVIDAD

RESUELVE EN TU CUADERNO: pag 16 - libro rutas matemáticas

IMPORTANTE TENER EN CUENTA:

2. fecha de entrega de la actividad desarrollada: LUNES 4 DE MAYO DEL 2020.

3. especificar: nombres, apellidos, grado del estudiante y materias.

--------------------------------------------------------------------------------------------------------------------------
24 – ABRIL - 2020 – SEMANA 5

OBJETIVOS:

· Opera sobre números desconocidos y encuentra las operaciones apropiadas al contexto para resolver problemas.

· Utiliza las operaciones y sus inversas en problemas de cálculo numérico

· Realiza combinaciones de operaciones, encuentra propiedades y resuelve ecuaciones en donde están involucradas

DIVISIÓN DE NÚMEROS NATURALES

En la división de números naturales se presentan dos casos dependiendo del residuo. Estos dos casos son: división exacta y división inexacta.

DIVISIÓN DE NÚMEROS NATURALES | Recurso educativo 679401 - Tiching

DIVISIÓN EXACTA DE NÚMEROS NATURALES:

La operación exacta es inversa a la multiplicación, ya que conociendo el producto y uno de los factores, esta permite hallar el otro factor. Una división es exacta cuando existe un número natural que multiplicado por el divisor da como resultado el dividendo. Así,

Dado a, b, c, € N, se define la división exacta como

a / b = c siempre que a = b * c

a se denomina dividendo, b divisor y c cociente. En este caso el residuo de la división es 0

por ejemplo, 24 / 8 = 3, ya que 3 * 8 = 24. Así, 24 es el dividendo, 8 el divisor y 3 el cociente.

DIVISIÓN INEXACTA DE NÚMEROS NATURALES:

Una división es inexacta cuando no existe un número natural que multiplicado por el divisor de como resultado el dividendo. Así,

Dados a, d, c, r € N, se define la división inexacta como

A se denomina dividendo, b divisor, c cociente y r residuo.

En este caso, el residuo de la división es diferente a 0

Por ejemplo:

Divisiones exactas y divisiones inexactas - Matemáticas de primaria

TERCERO HABANERAS: DIVISIÓN EXACTA E INEXACTA O NO EXACTA

PROPIEDADES DE LA DIVISIÓN:

la división en el conjunto de los números naturales, cumple únicamente con la siguiente propiedad.

La división es distributiva con respecto a la suma y resta. Así,

Dios es mi mejor amigo - Buscar con Google | Biblicas cristianas ...

--------------------------------------------------------------------------------------------------------------------------
20 - ABRIL - 20 --- SEMANA 5

OBJETIVOS:

Utiliza las propiedades de los números enteros y racionales y las propiedades de sus operaciones para proponer estrategias y procedimientos de cálculo en la solución de problemas.

Propone y utiliza diferentes procedimientos para realizar operaciones con números enteros y racionales

Argumenta de diversas maneras la necesidad de establecer relaciones y características en conjuntos de números (ser par, ser impar, ser primo, ser el doble de, el triple de, la mitad de, etc).

MULTIPLICACIÓN DE NÚMEROS NATURALES

Dados a, b, c, € N, se define la multiplicación o producto como a * b = c, donde a y b se denominan factores y c producto.

Por ejemplo, en la operación 7 * 4 = 28, 7 y 4 son los factores y 28 el producto .•

Características de la Multiplicación -【 Propiedades de la ...

PROPIEDADES DE LA MULTIPLICACIÓN DE NÚMEROS NATURALES:

•La multiplicación en el conjunto de los números naturales, cumple con las siguientes:

Propiedad conmutativa: El orden de los factores no varía el producto

Ejemplo: si a, b € N entonces, - a * b = b * a --- 9 * 4 = 4 * 9 en efecto 36 = 36

Con Antonio al aula: PROPIEDAD CONMUTATIVA DE LA MULTIPLICACIÓN

•Propiedad asociativa: El modo de agrupar los factores no varía el resultado de la multiplicación

Ejemplo: si a, b, c € N entonces, a * (b * c) = (a * b) *c --- 2*(5*4) = (2*5)*4

en efectos, 2 * 20 = 10 * 4 --- 40 = 40

Propiedades de la multiplicación: asociativa, conmutativa y ...

•Propiedad modulativa: El 1 (uno), es el elemento neutro de la multiplicación porque todo número multiplicado por él da el mismo número.

Ejemplo: si a € N entonces, a * 1 = 1 * a --- 7 * 1 = 1 * 7 = 7

Propiedades de la multiplicación: Distributiva, conmutativa ...

•Propiedad distributiva: La multiplicación de un número por una suma, es igual a la suma de las multiplicaciones de dicho número por cada uno de los sumandos.

Ejemplo: si a, b, c, € N entonces, a * (b + c) = (a * b) + (a * c)

5 * (6 + 4) = (5 * 4) + (5 * 6) --- en efecto, 5 * 10 = 30 + 20 --- 50 = 50

Propiedad distributiva: definición y ejemplos | Estudianteo

•Propiedad clausurativa: todos lo elementos que hacen parte de la multiplicación, ( factores y productos) pertenecen a los números naturales.

•Ejemplo: si a, b € N entonces, a * b € N --- 9 * 4 = 36 --- en efecto, 9 € N, 4 € N, 36 € N.

Características de los Números Naturales -【Propiedades】

No es seguro que todo el universo esté contenido en Pi, pero sí en ...

Infinity Symbol 1280*853 transprent Png Free Download - Text ...

Diga el débil fuerte soy*. Joel 3.10 -... - Vida Nueva Móstoles ...

IMPORTANTE TENER EN CUENTA:

2. fecha de entrega de la actividad desarrollada: VIERNES 24 ABRIL DEL 2020

3. especificar: nombres, apellidos, grado del estudiante y materias.

--------------------------------------------------------------------------------------------------------------------------

17 – ABRIL – 2020 – SEMANA 4

OBJETIVOS:

Utiliza las propiedades de los números enteros y racionales y las propiedades de sus operaciones para proponer estrategias y procedimientos de cálculo en la solución de problemas.

Propone y utiliza diferentes procedimientos para realizar operaciones con números enteros y racionales.

SUSTRACCIÓN DE NÚMEROS NATURALES

La sustracción es la operación inversa a la adicción. Es decir, conocidos la suma y uno de los sumandos, la sustracción permite hallar el otro sumando.

Dados a, b, c, ϵ N y a > b, se define la resta o sustracción como

a – b: c siempre que a: b + c

a se denomina minuendo, b sustraendo y c diferencia

c.2. SUSTRACCIÓN DE NÚMEROS NATURALES (Definición) - USO DE LAS ...

Action relationship of addition and subtraction, examples with ...

ACTIVIDAD

resuelve en tu cuaderno, la página 14 del libro rutas matemáticas:

1. Escribe en tu cuaderno = 0 ≠ según corresponda

62 – 13 ------ - 13 – 62
28 + 0 --------- 28 – 0
34 - (7+8) ------- (34 - 7) + 8
93 - (25 - 3) ------- (93 - 25) + 3
(33 - 12) – 7 ----- 33 - (12 + 7)

15 Versículos de la Biblia sobre la Adicción - DailyVerses.net

IMPORTANTE TENER EN CUENTA:

2. fecha de entrega de la actividad desarrollada: VIERNES 17 DE ABRIL DEL 2020.

3. especificar: nombres, apellidos, grado del estudiante y materias.

----------------------------------------------------------------------------------------------------------------------------------

13 - 04 - 20 --- SEMANA 4

OBJETIVOS:

Utiliza las propiedades de los números enteros y racionales y las propiedades de sus operaciones para proponer estrategias y procedimientos de cálculo en la solución de problemas.

Propone y utiliza diferentes procedimientos para realizar operaciones con números enteros y racionales.

Argumenta de diversas maneras la necesidad de establecer relaciones y características en conjuntos de números (ser par, ser impar, ser primo, ser el doble de, el triple de, la mitad de, etc.)

OPERACIONES EN EL CONJUNTO DE LOS NÚMEROS NATURALES

Los números naturales son aquellos que sirven para contar los elementos de un conjunto determinado. El conjunto de los números naturales se simboliza con la letra N y se determina por extensión de la siguiente manera.

▷ 🥇Conjunto de los【Números Naturales】Matemáticas , Algebra 🥇 ◁

En el conjunto de los números naturales se definen las siguientes operaciones: adicción, sustracción, multiplicación división, potenciación, radicación, y logaritmación.

ADICCIÓN DE NÚMEROS NATURALES:

Dados a, b, c, ϵ N, se define la suma o adicción como a+b=c, donde a y b se denominan sumandos y c suma o total.

Por ejemplo en la operación 11+8=19, 11 y 8 son los sumandos y 19 es la suma o total. La adicción en el conjunto de los números naturales cumple con las siguientes propiedades:

PROPIEDAD CLAUSURATIVA: los sumandos y el total pertenecen al conjunto de los números naturales

Ejemplo: a+b € N -- 2+5=7 -- 2€N, 5€N, 7€N

PROPIEDAD CONMUTATIVA: es irrelevante el orden de la operación o el orden de los sumandos

Ejemplo: a+b=b+a -- 2+5=5+2 en efecto 7

PROPIEDAD ASOCIATIVA: al operar con tres números o dígitos el modo de agruparlos no afecta el resultado.

Ejemplo: a+(b+c)=(a+b)+c -- 2+(5+3)=(2+5)+3 – en efecto 10=10

´PROPIEDAD MODULATIVA: el cero es el elemento neutro de la suma de enteros por que, cualquiera que sea el número natural a, se cumple que:

Ejemplo: a+0=0+a=a -- 5+0=0+5=5

ACTIVIDAD

Ejercicios propuestos

1. Agrupar y cambiar el orden de los términos para poder calcular las sumas mentalmente.

A. 98+3+97+2

B. 700+298+300+2

C. 106+15+4+10

D. 397+13+2+8

E. 326+4+14+6

F. 893+60+7+14

G. 7+135+13+15

H. 100+27+50+3

Ejemplo: 98+97+3+2=200 --- ojo debes realizarlo primero de manera mental y después verificar con la calculadora su valor.

1. Escribe en el espacio = 0 ≠ (no es igual a)

A. 58+23 ----- 23+58

B. 72+0+27 ----- 72+27

1. Determina el valor de cada expresión teniendo en cuenta las condiciones.

A. m+(n+t)+s ---- si m +n=6 y t+s=12

B. (a+b)+(c+d) ---- si a+b=12 y b+c=15

C. x+(z+n)+(w+p)+(k+l) ---- si x+z=12, n+k=8, w+l=20 y p=5

D. t+s+(a+b)+w+x ---- si w+s=12, a+b=20 y t+x=35

Ejemplo:

m+(n+t)+s ---- si m +n=6 y t+s=12

entonces - (m +n)=6 y (t+s)=12 = 18

IMPORTANTE TENER EN CUENTA:

2. fecha de entrega de la actividad desarrollada: LUNES 17 DE ABRIL DEL 2020.

3. especificar: nombres, apellidos, grado del estudiante y materias.

------------------------------------------------------------------------------------------------------------
03 – ABRIL – 2020

SISTEMA DE NUMERACIÓN DECIMAL

El sistema de numeración en base 10 está formada por las cifras 0, 1, 2, 3, 4, 5, 6, 7, 8, y 9; y recibe en nombre de sistema de numeración decimal, ya que cuenta con 10digitos teniendo en cuenta el numero 0.

Este sistema de numeración es posicional, lo cual significa que el valor de cada dígito depende de su posición dentro del número. En este sistema, cada 10 unidades representan una unidad de orden inmediato superior, así:

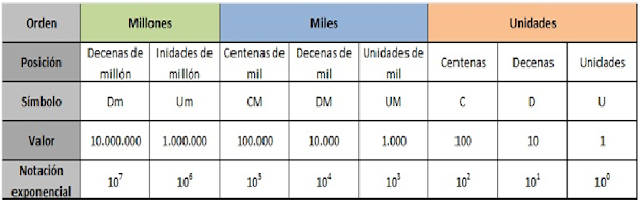
Herramientas matemáticas 6° y 7°: Sistemas de Numeración

De esta manera, un número en el sistema de numeración decimal puedes ser representado utilizando tres tipos de notación: polinómica, exponencial, y según el nombre de posición de cada cifra.

POLINÓMICA: el número de expresa teniendo en cuenta el valor de posición de cada una de las cifras. Por ejemplo, en número 719 puede ser expresado así:

700 + 10 + 9

EXPONENCIAL: el númerp se expresa teniendo en cuenta el valor de posición de cada una de sus cifras en forma exponencial. Por ejemplo, el número 254 puede ser expresado como:

(2 x $10^{2}\,$ ) + (5 x $10^{1}\,$ ) + (4 x $10^{0}\,$ )

SEGÚN EL NOMBRE DE POSICIÓN DE CADA CIFRA: en número se expresa teniendo en cuenta el nombre del valor de posición de cada una de sus cifras. Por ejemplo, el número 983 puede ser expresado como:

9C + 8D + 3D

NOTA: Siempre los números se ordenan de derecha a izquierda, desde el ultimo número hacia el primero así:

observa el siguiente vídeo:

observa el siguiente ejemplo:

ACTIVIDAD

Realiza los siguientes ejercicios propuestos en el libro rutas matemáticas, pág. 11.

IMPORTANTE TENER EN CUENTA:

2. fecha de entrega de la actividad desarrollada: LUNES 06 DE ABRIL DEL 2020.

3. especificar: nombres, apellidos, grado del estudiante y materias.

Dibujos Para Colorear Cristianos Con Versiculos Para Imprimir

----------------------------------------------------------------------------------------------------------------------------------

30 - MARZO - 2020

SOLUCIÓN DE LOS EJERCICIOS

1. Revisa con atención la solución de los ejercicios propuestos anteriormente; y si tienes un error rectifícalo:

Amén !!!!❤ | Ovejitas y ovejitas, Ovejas cristianas, Imágenes ...

----------------------------------------------------------------------------------------------------------------------------------

24 - MARZO-2020

SISTEMA DE NUMERACIÓN BINARIO Y SISTEMA DE NUMERACIÓN DECIMAL

Para convertir un numero en base 2 a base 10, es decir, de sistema binario a decimal, se debe tener en cuenta los siguientes pasos:

1. ubicar el número binario en orden, de listado, con el fin de que a cada cifra le corresponda una potencia de 2.

2. multiplicar cada cifra del numero binario por la potencia de 2 respectiva y sumar los productos obtenidos. El número que resulta sera el número binario representado en el sistema de numeración decimal.

2^0:	1

2^1:	2

2^2:	4

2^3:	8

2^4:	16

2^5:	32

2^6:	64

2^7:	128

2^8:	256

2^9:	512

2^10:	1.024

Se ubica el número binario de derecha a izquierda, en otras palabras, el ultimo número se multiplica con el primer del listado así:

101101_2:

_{PASO 1: se multiplica cada cifra del número por la potencia de dos respectiva y se suman los productos obtenidos. Como se muestra a continuación:}

2^0:	1 X 1: 1

2^1:	2 X 0: 0

2^2:	4 X 1: 4

2^3:	8 X 1: 8

2^4:	16 X 0: 0

2^5:	32 X 1: 32

PASO 2: sumamos : (1+0+4+8+0+32) esto es igual a: 45

PASO 3: entonces 101101_{2 es igual a:}(45)₁₀

ACTIVIDAD

1. En tu cuaderno escribir los siguientes números en base 10.

10₂

1₂

11₂

101₂

110₂

111₂

1000₂

1010₂

1001₂

10010₂

11011₂

110001₂

OTRO EJEMPLO: 10010₂

_{PASO 1: se multiplica cada cifra del número por la potencia de dos respectiva y se suman los productos obtenidos. Como se muestra a continuación:}

2^0:	1 X 0: 0

2^1:	2 X 1: 2

2^2:	4 X 0: 0

2^3:	8 X 0: 0

2^4:	16 X 1: 16

PASO 2: sumamos : (0+2+0+0+16) esto es igual a: 18

PASO 3: entonces 10010_{2 es igual a:}(₁₈)₁₀

NOTA: CONTINUA CON LOS EJERCICIOS PROPUESTOS ANTERIORMENTE EN TU CUADERNO, LIBRO RUTAS MATEMÁTICAS PAG-9

2. ACTIVIDAD: unir con una linea, las expresiones equivalente.

VI .580 .1001000100₂

DLXXX . 6000 .1011101110000₂

LIBRO RUTAS MATEMÁTICAS PAG-9

SUMA O MULTIPLICACIÓN DE DOS O MAS NÚMEROS EN BASE 2

para sumar o multiplicar dos o mas números en base 2, se debe tener en cuenta las siguientes sumas y productos fundamentales:

0 + 0=0 0 X 0=0

0 + 1=1 0 X 1=0

1 + 0=1 1 X 0=0

1 + 1=10 1 X 1=1

EJEMPLO:

Resultado de imagen para suma de numeros binarios

Resultado de imagen para multiplicacion de numeros binarios 1001 por 101

3. ACTIVIDAD: resolver las siguientes operaciones.

1001 + 1001 1oo X 100

11110 + 11111 101 X 100

LIBRO RUTAS MATEMÁTICAS PAG-9

NOTA: REALIZA TODOS LOS EJERCICIOS PROPUESTOS DEL LIBRO RUTAS MATEMÁTICAS PAG-9, EN TU CUADERNO.

LINK DE EXPLICACIÓN DEL SISTEMA DE NUMERACIÓN BINARIO

EL SIGUIENTE VÍDEO ES PUBLICADO CON EL PROPÓSITO, DE QUE LOS ESTUDIANTES DE GRADO SEXTO, COMPRENDAN LA TEMÁTICA :

https://www.youtube.com/watch?v=n6etabbWK80

IMPORTANTE TENER EN CUENTA:

2. fecha de entrega de la actividad desarrollada: JUEVES 2 DE ABRIL DEL 2020.

3. especificar: nombres, apellidos, grado del estudiante y materias.

------------------------------------------------------------------------------------------------------------

HISTORIA DE LAS MATEMÁTICAS

https://www.tiki-toki.com/timeline/entry/1264750/EVOLUCIN-DE-LAS-MATEMTICAS/

SISTEMA DE NUMERACIÓN BINARIO

Un sistema de numeración recibe su nombre a partir de la cantidad de símbolos que se usan en la escritura de números. a este número se le denomina BASE. por ejemplo, el sistema de numeración en base 6, se compone de las cifras 0, 1, 2, 3, 4, 5.

El sistema de numeración binario es un sistema en el cual se utilizan únicamente dos dígitos: 0 y 1.

Para convertir un número en base 10 a base 2, es decir, de sistema decimal, a binario, es necesario realizar divisiones sucesivas entre 2, teniendo en cuenta el último cociente y los residuos respectivos de cada una de las divisiones realizadas.

libro rutas matemáticas pag. 8

recordemos las partes de la división:

Resultado de imagen para partes de la division

ver el siguiente vídeo:

https://www.youtube.com/watch?v=QUiURUkNxC4

Resultado de imagen para sistema de numeracion binario base de 2 numero 50

ejemplo:

al observar la imagen, se esta aplicando el sistema sistema de numeración binario, donde el numero 50 hace parte del sistema decimal, y el numero 2 es la base, por lo tanto se realizan divisiones sucesivas entre 2; hasta que el resto quede en 0 o 1.

entonces 50: 1100102 ----- este número 2 es la base y siempre

ACTIVIDAD

realiza los siguientes ejercicios:

1. escribe los siguientes números en base 2

9 25
92 110
227 1.320
17 50
309 458
530 3.020

libro rutas matemáticas pag. 9 (ejercicio P)

IMPORTANTE TENER EN CUENTA:

1. tomar foto de la actividad desarrollada en el cuaderno, al correo murilloviviana82@gmail.com

2. fecha de entrega de la actividad desarrollada: MARTES, 24 DE MARZO DEL 2020.

3. nombre completo del estudiante y el grado

NOTA: todo la explicación anterior debe ir registrada en el cuaderno, por favor enviar a mi correo (murilloviviana82@gmail.com - especificar el nombre, apellido y grado del estudiante ) la solución de los puntos anteriores a través de una fotografía.

3 comentarios:

Unknown19 de marzo de 2020, 7:13
hola profe, soy Sara Maryanna y queria saber lo de la pagina 9.Muchas Gracias, si me puede ayudar con eso.
ResponderEliminar
Respuestas
Unknown19 de marzo de 2020, 7:14
ya que no tengo el libro.
ResponderEliminar
Respuestas
Sociales24 de marzo de 2020, 10:52
Hola buenas tardes profesora le habla la mamá de Joan Silva castillo hay le envió la tarea
ResponderEliminar
Respuestas

Añadir comentario

INSTITUTO LA RIVERA

Páginas

MATEMÁTICAS

3 comentarios:

BIENVENIDO GRADO SEXTO

Denunciar abuso