14/08/2020
– SEMANA 9
CUADRILÁTERO
Dale click al siguiente link:
https://drive.google.com/file/d/1Kx0ZJtQEchbK_8yxPRXFb1V3du2NtLN_/view?usp=sharing
---------------------------------------------------------------------------------------------------------------------------------
31– 07 – JULIO – 2020 – SEMANA 8
CUADRILÁTEROS
Dale click al siguiente link:
https://drive.google.com/file/d/1ijOsDWVsVmhjRykoj6r0sBtaJfSuuDru/view?usp=sharing
---------------------------------------------------------------------------------------------
10-JULIO–2020–SEMANA-7
TRIÁNGULOS
Dale click al siguiente link:
https://drive.google.com/file/d/1qki7jJfT9fGqKNQlhDN494IJFZv282RM/view?usp=sharing
------------------------------------------------------------------------------------------------------------
25 - JUNIO – 2020 – SEMANA 6
TRIÁNGULOS
Un triángulo es el polígono que resulta de unir 3 puntos con líneas rectas. Todo triángulo tiene 3 lados (a, b y c), 3 vértices (A, B y C) y 3 ángulos interiores (a, b y g).
Los triángulos podemos clasificar los según 2 criterios:
Según la medida de sus lados
- Equilátero: los 3 lados son iguales
- Isósceles: tienen 2 lados iguales y un lado distinto
Escaleno: los 3 lados son distintos
Según la medida de sus ángulos:
- Acutángulo: los 3 ángulos miden menos de 90 grados
Rectángulo: tiene uno de sus lados recto, (90 grados)
Obtusángulo: el ángulo interior mide (más de 90 grados):
---------------------------------------------------------------------------------------------------------
18- JUNIO – 2020 – SEMANA 5
OBJETIVOS:
· ·
Utiliza y explica diferentes estrategias
(desarrollo de la forma
plantillas) e instrumentos (regla, compás
o software) para la
construcción de figuras planas y cuerpos.
·
Construye plantillas para cuerpos
geométricos dadas sus
medidas.
POLÍGONOS

ACTIVIDAD
Resuelve:
pag 131 – libro Rutas Matemáticas
Responde:
·
¿Cómo se llama un polígono de cuatro
lados?
·
¿Cómo se llama un polígono de ocho lados?
·
¿Cómo se llama un polígono con todos sus
lados iguales?
·
¿Cómo se llama un polígono de seis lados?
·
Por medio de 3 mapas mentales, explica la clasificación
de los polígonos; según el número de sus lados, según su forma, y según la
medida de sus lados.
IMPORTANTE TENER EN CUENTA:
1. tomar foto de la transcripción de la
información y la actividad desarrollada en el cuaderno, enviarla al
correo murilloviviana82@gmail.com. Por favor enviar un solo correo con
todas las fotos relacionadas a mis áreas.
2. fecha de entrega de la actividad
desarrollada: LUNES 22 DE JUNIO
DEL 2020.
3. especificar: nombres, apellidos,
grado del estudiante y materias.
--------------------------------------------------------------------------------------------------------
11 – JUNIO – 2020 – SEMANA:
10
POLÍGONOS
CLASE EN EL SIGUIENTE LINK:
------------------------------------------------------------------------------------------------------------------------------------
02/06/2020 – SEMANA 9
SEGUNDO PERIODO
Ejes temáticos:
Generalidades
de la geometría
1. Conceptos
básicos
2. Polígonos
Generalidades
de la geometría
1. Triángulos
Grafica del segundo periodo (1 hoja )
Ejemplos:


OBJETIVOS:
- Representa y construye formas bidimensionales y tridimensionales con el apoyo en instrumentos de medida apropiados.
- Construye cuerpos geométricos con el apoyo de instrumentos de medida adecuados.
Construcción
de perpendiculares y construcción de paralelas
Construcción
de rectas perpendiculares:
Con
regla y compás
- Supongamos que tenemos una recta r y un punto P y queremos trazar una recta perpendicular a r que pase por el punto P.
- Marcamos dos puntos A y B sobre la recta r.
- Luego trazamos dos arcos de circunferencias con centros en A y B y que pasen por el punto P, tratando que los arcos se intersecten también del otro lado.
- Marcamos el punto de intersección Q y trazamos la recta s de tal manera que pase por los puntos P y Q.
Construcción
de paralelas con
compás :
- Desde el punto P y con una abertura cualquiera del compás, se traza un arco que corte a la recta r. De esta forma obtenemos el
- Desde el punto 1 y con la misma abertura del compás, se traza otro arco que tendrá que pasar por el punto P y cortar a la recta r. Se obtiene el punto 2.
- Con la ayuda del compás, se toma la distancia que hay entre el punto 2 y el punto P. Se lleva a partir del punto 1. Se obtiene el punto 3.
- Se unen los puntos P y 3 y obtengo la recta que pasa por P y es paralela a la recta r.
ACTIVIDAD
Responde en tu cuaderno.
¿Qué
son líneas perpendiculares? – realiza un ejemplo.
Construye una recta perpendicular, con ayuda de una escuadra.
Construye una recta perpendicular, con ayuda de un compás.
¿Qué son líneas paralelas? – realiza un ejemplo.
Construye una recta paralelas, con ayuda de unas escuadras.
Construye una recta paralelas, con ayuda de un compás y regla.
Construye una recta perpendicular, con ayuda de una escuadra.
Construye una recta perpendicular, con ayuda de un compás.
¿Qué son líneas paralelas? – realiza un ejemplo.
Construye una recta paralelas, con ayuda de unas escuadras.
Construye una recta paralelas, con ayuda de un compás y regla.
Realiza la página 126 del libro rutas matemáticas.
IMPORTANTE TENER EN CUENTA:
1. tomar foto de la transcripción de la información y la actividad desarrollada en el cuaderno, enviarla al correo murilloviviana82@gmail.com. Por favor enviar un solo correo con todas las fotos relacionadas a mis áreas.
2. fecha de entrega de la actividad desarrollada: MARTES 09 DE MAYO DEL 2020.
3. especificar: nombres, apellidos, grado del estudiante y materias.
--------------------------------------------------------------------------------------------------------------------------
07 – MAYO – 2020 – SEMANA 8
OBJETIVOS:
Identifica los elementos que componen las figuras y cuerpos geométricos.
Construye cuerpos geométricos con el apoyo de instrumentos de medida
adecuados.
CONCEPTOS BÁSICOS
ACTIVIDAD
A través de un mapa conceptual y ejemplos,
Responde:
- ¿Qué es punto en geometría?
- ¿Qué es recta en geometría?
- ¿Qué es plano en geometría?
- ¿Qué son puntos colineales?
- ¿Qué son puntos coplanares?
- ¿Qué son rectas intersecantes o rectas secantes?
- ¿Qué son
rectas coplanares geometría?
- ¿Qué son rectas concurrentes geometría?
Resuelve:
pag 128 – libro Rutas Matemáticas
IMPORTANTE TENER EN CUENTA:
1. tomar foto de la transcripción de la
información y la actividad desarrollada en el cuaderno, enviarla al
correo murilloviviana82@gmail.com. Por favor enviar un solo correo con
todas las fotos relacionadas a mis áreas.
2. fecha de entrega de la actividad
desarrollada: LUNES 18 DE
ABRIL DEL 2020.
3. especificar: nombres, apellidos,
grado del estudiante y materias.
--------------------------------------------------------------------------------------------------------------------------
07 – MAYO – 2020 – SEMANA 7
OBJETIVOS:
Identifica los elementos que componen las figuras y cuerpos
geométricos.
Construye cuerpos geométricos con el apoyo de instrumentos
de medida adecuados.
CONCEPTOS BÁSICOS
Los conceptos básicos en la geometría son: punto, recta, y
plano.
La marca que deja un lápiz bien afilado en una hoja, sugiere
la idea de punto. El punto no
tiene tamaño, solo tiene posición. Estos se simbolizan con letras mayúsculas.
Un cordón bien estirado o la marca que deja un lápiz al
pasarlo por le borde de la regla, sugiere la idea de línea recta. La línea
recta está formada por una sucesión de puntos que se prolongan en una sola dirección.

Para representar una recta, se trazan flechas, en ambos
sentidos, estos indican que se prolongan indefinidamente. Para nombrar una
recta, se marca dos puntos sobre ella y se dibuja una doble flecha encima de
las letras que los simbolizan. También se pueden nombrar con letras mayúsculas.

Una hoja de papel, la superficie de una caja o el piso, sugieren
la idea de plano. Un plano se prolonga indefinidamente en todas las direcciones,
está formado por infinitos puntos y no tiene grosor.
Para simbolizar un plano, se marcan tres puntos sobre él.

Los puntos se pueden relacionar según su posición, así:
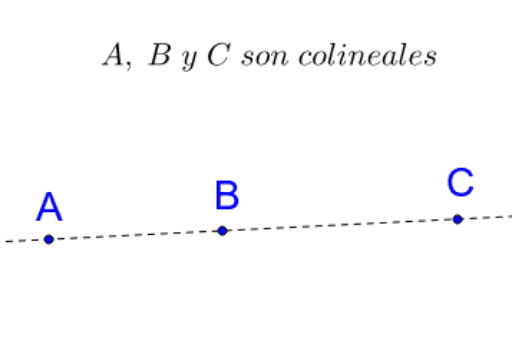
·
Si los puntos pertenecen a la misma recta, se le
llaman colineales.
Si los
puntos pertenecen al mismo plano, se le llaman coplanares.

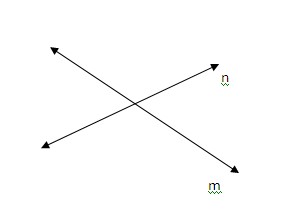
De manera similar, las rectas se pueden relacionar así:
Dos rectas que se cortan en un punto, se llaman rectas
intersecantes o rectas secantes.
·
Dos rectas que pertenecen a un mismo plano, se
llaman coplanares.
·
Tres o mas rectas coplanares que se intersecan
en el mismo punto se llaman rectas concurrentes.

23 – ABRIL – 2020 – SEMANA 6
OBJETIVOS:
Propone patrones de comportamiento numéricos y expresa verbalmente o por escrito los procedimientos matemáticos
Trabaja sobre números desconocidos y con esos números para dar respuestas a los problemas.
MASA
ACTIVIDAD
1. investiga ¿que es masa?
2. investiga la biografía de ISAAC NEUWTON
3. ¿como descubrió ISAAC NEUWTON la fuerza gravitacional?
4. investiga ¿que es la fuerza gravitacional?
RESUELVE: pag 122 - libro rutas matemáticas
NOTA: PARA PASAR LAS CANTIDADES ANTERIORES A GRAMOS DEBES TENER EN CUENTA LA SIGUIENTE IMAGEN:

IMPORTANTE TENER EN CUENTA:
1. tomar foto de la transcripción de la información y la actividad desarrollada en el cuaderno, enviarla al correo murilloviviana82@gmail.com. Por favor enviar un solo correo con todas las fotos relacionadas a mis áreas.
2. fecha de entrega de la actividad desarrollada: LUNES 4 DE MAYO DEL 2020.
3. especificar: nombres, apellidos, grado del estudiante y materias.
---------------------------------------------------------------------------------------------------------23 – ABRIL – 2020 – SEMANA 5
OBJETIVOS:
Propone patrones de comportamiento numéricos y expresa verbalmente o por escrito los procedimientos matemáticos
Trabaja sobre números desconocidos y con esos números para dar respuestas a los problemas.
MASA
§¿por qué las manzanas caen de
manera perpendicular al suelo?
§¿por que no cae hacia arriba o hacia un costado?
R- esta fuerza de atracción de llama gravedad.
- Todos los objetos son atraídos por la tierra, por una fuerza directamente proporcional al producto de su masa.
- Cuanto mayor sea la masa de un objeto, mayor será la atracción que tendrá hacia la tierra.
¿Qué es masa?
La masa en un atributo de los cuerpos.
Por ejemplo, si se compara un ladrillo y una semilla se puede notar que la masa
del ladrillo es mayor que la masa de la semilla.
- La unidad fundamental de la masa es el gramos y se simboliza con la letra G.
- La Masa es la medida que indica la cantidad de materia que tiene un cuerpo.
Al
igual que el metro, el gramo tiene múltiplos y submúltiplos así:
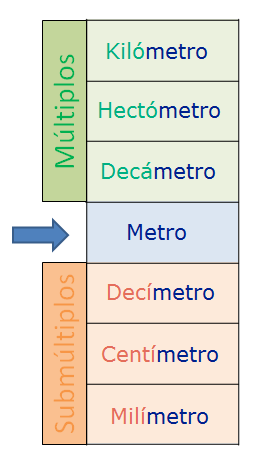
para establecer equivalencia entre las unidades de peso, se produce en forma similar a la planteada en unidades de longitud . El esquema empleado en este caso, es el siguiente:

---------------------------------------------------------------------------------------------------------
16 – ABRIL – 2020 – SEMANA 4
OBJETIVOS:
- Propone y desarrolla estrategias de estimación, medición y cálculo de diferentes cantidades (ángulos, longitudes, áreas, volúmenes, etc.) para resolver problemas.
- Estima el resultado de una medición sin realizar la, de acuerdo con un referente previo y aplica el proceso de estimación elegido y valora el resultado de acuerdo con los datos y contexto de un problema.
- Estima la medida de longitudes, en presencia o no de los objetos y decide sobre la conveniencia de los instrumentos a utilizar, según las necesidades de la situación.
PERIMETRO
El perímetro de una figura se puede entender como la longitud de la línea que forma su contorno.
Por ejemplo, si se pone una cuerda alrededor de una figura y luego se estira,
la medida de la cuerda determina el perímetro.
Observa con atención el siguiente vídeo:



Si la figura está limitada por lados rectos, el
perímetro corresponde a la suma de sus longitudes.
Ejemplo:
Para cercar un terreno se decidió poner una vuelta de
alambre a su alrededor. Si el metro de alambre cuesta $2.500, ¿cuánto
dinero se necesita para cercarlo?
ACTIVIDAD
Resuelve los siguientes ejercicios de la página 121

IMPORTANTE TENER EN CUENTA:
1. tomar foto de la transcripción de la
información y la actividad desarrollada en el cuaderno, enviarla al
correo murilloviviana82@gmail.com. Por favor enviar un solo correo con
todas las fotos relacionadas a mis áreas.
2. fecha de entrega de la actividad
desarrollada: VIERNES 17
DE ABRIL DEL 2020.
3. especificar: nombres, apellidos,
grado del estudiante y materias.
--------------------------------------------------------------------------------------------------------------------------02 - ABRIL - 2020
LONGITUD
La longitud es una magnitud que se mide en una dimensión. Cuando se habla del ancho, el largo, la altura y la distancia, se hace referencia a la longitud.
Observa con atención el siguiente vídeo:
responde a las preguntas:
· ¿Qué es metro?
· ¿Cuál es la unidad de longitud más importantes? ¿con que letra se representa? Realiza un ejemplo.
· ¿para qué sirve un metro?
· Nombra las tres unidades de medida, que permiten medir objetos pequeños.
UNIDADES DE LONGITUD
La unidad fundamental para medir longitudes es el metro, se simboliza con la letra m.
Existen unidades de orden superior al metro llamadas múltiplos y otros de orden inferior llamados submúltiplos.

CONVERSIONES:
Una longitud expresada en una unidad determinada, se puede expresar de manera equivalente en otra unidad de longitud. Por ejemplo, 5 km es equivalente a 5.000 m
Para el anterior ejercicio se utilizó la siguiente gráfica:
Si queremos convertir desde una unidad que está "separada" de otra, debemos "acumular las operaciones" según "subimos" o "bajamos" de la escalera.

Ejemplos:
- Para pasar de metro a centímetro bajamos 2 peldaños, por tanto, debemos multiplicar X10 y X10, es decir, multiplicaremos X100 (1m=100cm, 5m=500cm)
- Para pasar de metro a kilómetro subimos 3 peldaños, por tanto, debemos dividir ÷10, ÷10 y ÷10, es decir dividiremos ÷1000 (1000m=1km, 3000m=3km)
Observa el siguiente vídeo:
ACTIVIDAD
Realiza los siguientes ejercicios, planteados en el libro rutas de las matemáticas pág. 121.
IMPORTANTE TENER EN CUENTA:
1. tomar foto de la transcripción de la información y la actividad desarrollada en el cuaderno, enviarla al correo murilloviviana82@gmail.com. Por favor enviar un solo correo con todas las fotos relacionadas a mis áreas.
2. fecha de entrega de la actividad desarrollada: VIERNES 03 DE ABRIL DEL 2020.
3. especificar: nombres, apellidos, grado del estudiante y materias.

-------------------------------------------------------------------------------------------------------------------------
AMPLITUD
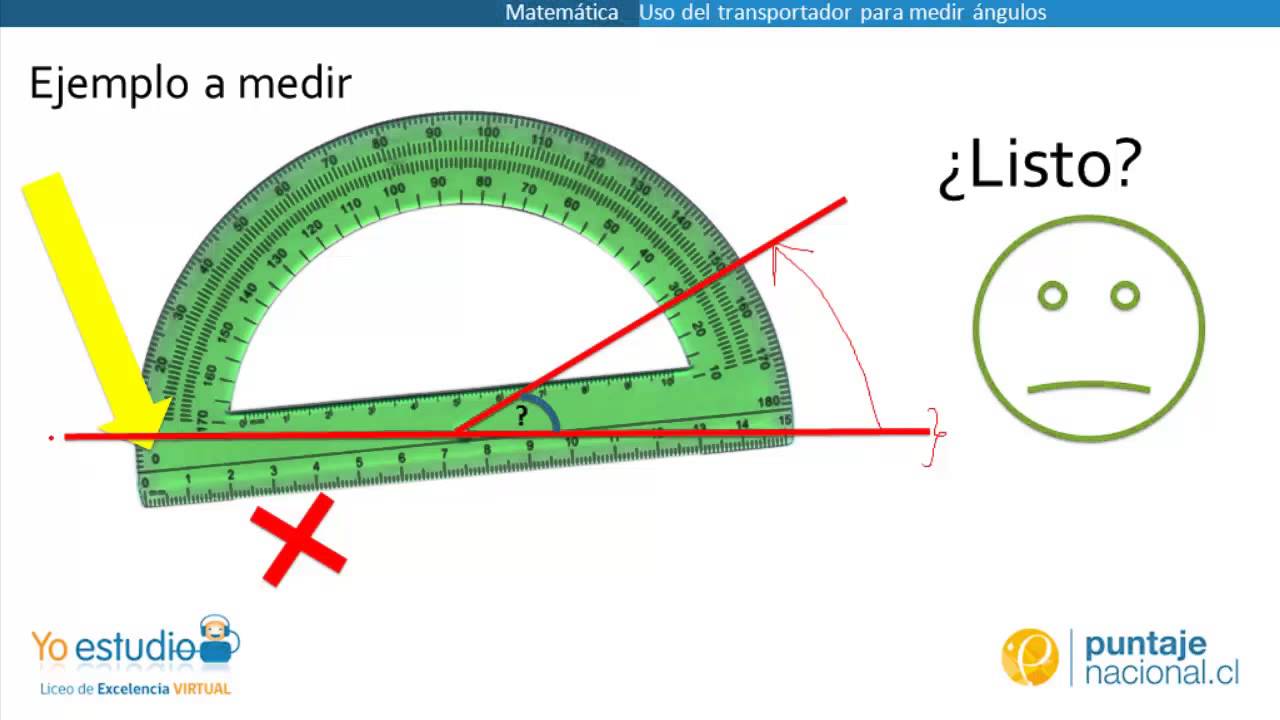
El instrumento que se usa para medir ángulos es el transportador.
Para medir un ángulo, se hace coincidir el centro del transportador con el vértice del ángulo, se hace coincidir el centro del transportador con el vértice del ángulo, y el cero (0°) del transportador con uno de sus lados. luego, se observa el número por el cual pasa el otro lado. Ese número de grados es la amplitud del ángulo. Por ejemplo:
partes del transportador:

Uso correcto del transportador:

Uso incorrecto transportador:
Observa el siguiente vídeo:
CLASIFICACIÓN DE ÁNGULOS
Los ángulos se pueden clasificar teniendo en cuenta tres criterios: amplitud, suma de amplitudes y posición.
clasificación de ángulos según su amplitud
De acuerdo con su amplitud, los ángulos se pueden clasificar como se muestra a continuación.
Ángulo agudo: mide menos de 90°

Ángulo recto: mide exactamente 90°
Ángulo obtuso: mide mas de 90° pero menos de 180°

Ángulo llano: mide exactamente 180°
Ángulo cóncavo: mide más de 180° pero menos de 360°
Ángulo completo: mide exactamente 360°
clasificación de ángulo según la suma de sus medidas
De acurdo con la suma de sus medidas, dos ángulos pueden ser complementarios o suplementarios.
Ángulos complementarios: la suma de sus medidas es 90°. por ejemplo:
Si el angulo uno mas el angulo dos es igual a 90°.
Si el angulo uno es el complemento del angulo dos o el angulo dos es el complemento del angulo uno.
Ángulos suplementarios: la suma de sus medidas es 180° . por ejemplo:
Si el angulo uno mas el angulo dos es igual a 180° se dice que:
El angulo uno es el suplemento del angulo dos o el angulo dos es el suplemento del angulo uno.
clasificación de ángulos según su posición
Según su posición, dos ángulos pueden ser consecutivos, Adyacentes u opuestos por el vértice.
Ángulos consecutivos: tiene el mismo vértice y uno de sus lados es común.
Ángulos adyacentes: son consecutivos y sus lados no comunes están en la misma recta.
Ángulo opuestos por el vértice: están formados entre dos rectas que se intersecan en un punto. Dicho punto es el vértice de los ángulos.
ACTIVIDAD
Realiza el ejercicio número 1 del libro rutas matemáticas, pag 119.
Construir un ángulo para cada condición. Luego, clasificarlos.
Ángulo ABC, que mida menos de 90°.
Ángulo N, que mida entre 120° y 140°.
Ángulo A, que mide entre 270° y 300°.
Ángulo MOP, que mida entre 110° y 150°.
Ángulo B, que mida entre 180° y 210°.
Ángulo OPQ, que mida entre 98° y 120°.
IMPORTANTE TENER EN CUENTA:
1. tomar foto de la actividad desarrollada en el cuaderno, al correo murilloviviana82@gmail.com
2. fecha de entrega de la actividad desarrollada: MARTES, 24 DE MARZO DEL 2020.
3. nombre completo del estudiante y el grado
NOTA: todo la explicación anterior debe ir registrada en el cuaderno, por favor enviar a mi correo (murilloviviana82@gmail.com - especificar el nombre, apellido y grado del estudiante ) la solución de los puntos anteriores a través de una fotografía.





















No hay comentarios:
Publicar un comentario